1. 다익스트라(Dijkstra) 란?
- 다익스트라 알고리즘이란 하나의 그래프에서의 최단 경로 탐색 알고리즘이며, 우리가 흔히 알고있는 동적계획법 즉 다이나믹 프로그래밍을 활용한 최단경로 탐색 알고리즘이다.
- 한 정점에서 모든 정점까지의 최단거리를 구할 때 사용하며, 주어진 그래프중에서 음의 가중치가 없는 그래프에서 사용 가능하다. 음의 가중치가 있을 경우 벨만-포드 알고리즘을 사용하여 해결할 수 있다.
2. Default Logic
다익스트라 알고리즘 동작 반복 과정
1. 방문하지 않은 정점 중 가장 가중치 값이 작은 정점을 방문한다.
2. 현재 위치한 정점을 거쳐 다른 노드로 넘어가는 가중치 값을 계산하여 최소 비용을 갱신한다.
3. 위의 과정을 목표한 노드에 도달 할 때까지 반복한다.
이해를 돕기 위해 시각적으로 정리해 보았다.
시작 노드를 1번 노드, 목표한 도착노드를 4번 노드라고 가정한 후 진행할 것이다.
먼저 처음 시작할 때에는 거리 테이블을 엄청나게 큰 값 INF(Infinite) 무한대 값으로 초기화 한후 시작한다.
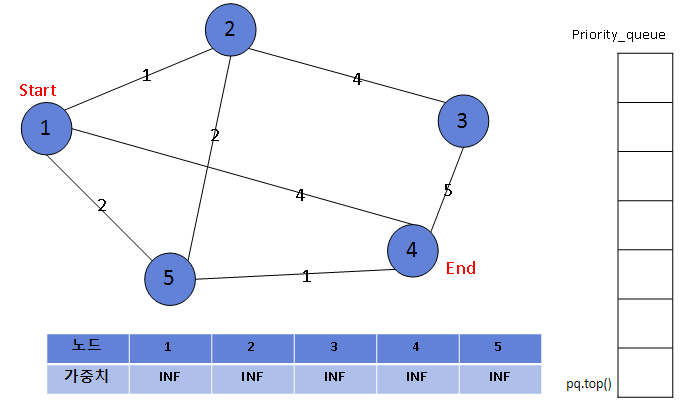
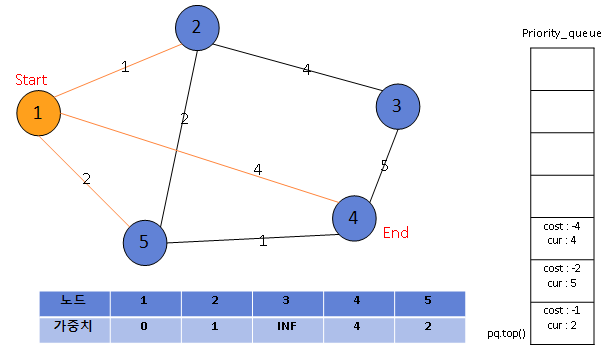
시작하는 노드인 1번 노드에 위치할 때 1번 노드의 가중치를 0으로 설정해주고 1과 근접해있는 노드들의 가중치를 확인해준다. 만약 주변의 노드의 가중치보다 (현재 노드의 가중치 + 인접 노드로 가는 가중치)가 더 작다면 priority_queue에 넣어준다. 지금 상태는 주변 인접노드들이 전부 INF값이기 때문에 다 들어간다.
대신 가중치에 -를 붙혀 오름차순으로 정리해 준다.

가장 인접한 2번, 4번, 5번 노드의 가중치를 확인했을 때 2번 노드로 가는 가중치가 가장 적기 때문에 2번 노드에 방문한다.
2번 노드에 도착한 후 2번 노드와 인접한 노드인 3번 5번 노드를 탐색한다. 3번노드로 가는 방법의 가중치는 1번에서 2번을 가는 가중치에 2번에서 3번을 가는 가중치를 거쳐야하기 때문에 5고 현재 3번 노드의 가중치는 INF이기 때문에 이또한 priority_queue에 넣어준다. 5번 노드로 가는 방법은 1 > 2 + 2 > 5 이기 때문에 가중치가 3이지만 1에서 5번 노드로 가는 방법이 가중치 2로 존재하기 때문에 넣지 않는다.

똑같이 가중치가 가장 낮은 5번노드로 이동후 방문하지 않은 간선을 확인한다. 4번노드로 이동하는 간선의 가중치를 확인 했을 때 1 > 5 > 4로 가는 방법은 3의 가중치를 가지고 1 > 4로 가는 방법은 4의 가중치를 가지기 때문에 더 작은 값인 1 > 5 > 1로 가는 방법을 pq에 넣게 된다.

우리가 목표한 노드는 4번 노드인데 priority_queue에 보면 cur이라는 값에 4번 노드를 가진 값이 두개가 들어있다. 가장 가중치가 작은 top에 위치한 순서를 수행하게 되면 그 뒤에 있는 가중치 4짜리는 저절로 가지치기 당하게 된다.

이렇게 해서 모든 한 점에서 시작하여 모든 인접한 간선을 조사한 후 가장 최단경로로 갈 수 있는 경우의 수를 조사하는 알고리즘이 다익스트라 알고리즘이다.
백준에 있는 다익스트라 알고리즘을 활용하여 푸는 문제 중 1753번 최단경로 라는 문제의 정답을 약간 변형해서 가져왔다.
대표적인 다익스트라 문제이며 가장 스탠다드한 풀이이다.
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f; // 시작 노드에서 해당 노드까지의 경로가 없는 경우의 비용
#define MAX_VERTEX 1001 // 최대 vertex 개수
#define MAX_EDGE 1001 // 최대 edge 개수
int v, e, start_node;
//최소 비용 배열
int d[MAX_VERTEX];
//간선 정보를 담은 vector
//index : 시작노드
//value : pair<비용, 도착 노드> 목록
vector<pair<int, int>> edge[MAX_EDGE];
void dijkstra(int start_node) {
//시작 노드에서 시작 노드로 가는 비용은 0
d[start_node] = 0;
//시작 노드부터 어떤 도착 노드까지의 최소 비용을 제시하는 간선 목록
//pair<비용, 도착 노드> 형식의 우선순위 큐이다.
priority_queue<pair<int, int>> pq;
//시작 노드에서 시작 노드로 가는 경로와 비용을 pq에 삽입;
pq.push({0, start_node});
//pq의 모든 경로를 확인할 때 까지 반복
while(!pq.empty()) {
int cur = pq.top().second;
int cost = -pq.top().first; //오름차순 정렬을 위해 -를 붙혀서 넣어줬기 때문에 다시 원래값으로 돌림
pq.pop();
if(d[cur] < cost) {
continue;
}
for(int i = 0; i < edge[cur].size(); ++i) {
int next = edge[cur][i].second;
int nextCost = cost + edge[cur][i].first;
if(d[next] > nextCost) {
d[next] = nextCost;
pq.push({-nextCost, next}); //오름차순 정렬을 위해 -를 붙혀서 넣어줌
}
}
}
}
int main() {
cin >> v >> e;
cin >> start_node;
for(int i = 1; i <= v; i++) {
d[i] = INF;
}
while(e--) {
int start, end, cost;
cin >> start >> end >> cost;
edge[start].push_back({cost, end});
}
dijkstra(start_node);
for(int i = 1; i < v + 1; ++i) {
if(d[i] == INF) {
cout << "INF" << "\n";
}
else {
cout << d[i] << "\n";
}
}
}3. 시간복잡도
간선의 수를 E(Edge), 노드의 수를 V(Vertex)라고 했을 때 O(E logV)가 된다.
우선순위 큐에서 꺼낸 노드는 서로 인접한 노드만 탐색하므로 최악의 경우라도 총 간선 수인 E만큼만 반복한다. 즉 하나의 간선에 대해서는 O(logE)이고, E는 V2보다 항상 작기 때문에 E개의 간선을 우선순위 큐에 넣었다 빼는 최악의 경우에 대해서는 O(E logV)가 된다.
4. 추천 문제
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 유니온 파인드 / Union-Find (0) | 2023.10.01 |
|---|---|
| [Algorithm] 이분탐색 / Binary Search (0) | 2023.09.25 |
| [Algorithm] 위상정렬 / Topological Sort (0) | 2023.09.22 |
| [Algorithm] 투포인터 / Two Pointers (0) | 2023.08.21 |
| [Algorithm] 동적 계획법 / Dynamic Programming (0) | 2023.06.19 |
1. 다익스트라(Dijkstra) 란?
- 다익스트라 알고리즘이란 하나의 그래프에서의 최단 경로 탐색 알고리즘이며, 우리가 흔히 알고있는 동적계획법 즉 다이나믹 프로그래밍을 활용한 최단경로 탐색 알고리즘이다.
- 한 정점에서 모든 정점까지의 최단거리를 구할 때 사용하며, 주어진 그래프중에서 음의 가중치가 없는 그래프에서 사용 가능하다. 음의 가중치가 있을 경우 벨만-포드 알고리즘을 사용하여 해결할 수 있다.
2. Default Logic
다익스트라 알고리즘 동작 반복 과정
1. 방문하지 않은 정점 중 가장 가중치 값이 작은 정점을 방문한다.
2. 현재 위치한 정점을 거쳐 다른 노드로 넘어가는 가중치 값을 계산하여 최소 비용을 갱신한다.
3. 위의 과정을 목표한 노드에 도달 할 때까지 반복한다.
이해를 돕기 위해 시각적으로 정리해 보았다.
시작 노드를 1번 노드, 목표한 도착노드를 4번 노드라고 가정한 후 진행할 것이다.
먼저 처음 시작할 때에는 거리 테이블을 엄청나게 큰 값 INF(Infinite) 무한대 값으로 초기화 한후 시작한다.

시작하는 노드인 1번 노드에 위치할 때 1번 노드의 가중치를 0으로 설정해주고 1과 근접해있는 노드들의 가중치를 확인해준다. 만약 주변의 노드의 가중치보다 (현재 노드의 가중치 + 인접 노드로 가는 가중치)가 더 작다면 priority_queue에 넣어준다. 지금 상태는 주변 인접노드들이 전부 INF값이기 때문에 다 들어간다.
대신 가중치에 -를 붙혀 오름차순으로 정리해 준다.

가장 인접한 2번, 4번, 5번 노드의 가중치를 확인했을 때 2번 노드로 가는 가중치가 가장 적기 때문에 2번 노드에 방문한다.

2번 노드에 도착한 후 2번 노드와 인접한 노드인 3번 5번 노드를 탐색한다. 3번노드로 가는 방법의 가중치는 1번에서 2번을 가는 가중치에 2번에서 3번을 가는 가중치를 거쳐야하기 때문에 5고 현재 3번 노드의 가중치는 INF이기 때문에 이또한 priority_queue에 넣어준다. 5번 노드로 가는 방법은 1 > 2 + 2 > 5 이기 때문에 가중치가 3이지만 1에서 5번 노드로 가는 방법이 가중치 2로 존재하기 때문에 넣지 않는다.

똑같이 가중치가 가장 낮은 5번노드로 이동후 방문하지 않은 간선을 확인한다. 4번노드로 이동하는 간선의 가중치를 확인 했을 때 1 > 5 > 4로 가는 방법은 3의 가중치를 가지고 1 > 4로 가는 방법은 4의 가중치를 가지기 때문에 더 작은 값인 1 > 5 > 1로 가는 방법을 pq에 넣게 된다.

우리가 목표한 노드는 4번 노드인데 priority_queue에 보면 cur이라는 값에 4번 노드를 가진 값이 두개가 들어있다. 가장 가중치가 작은 top에 위치한 순서를 수행하게 되면 그 뒤에 있는 가중치 4짜리는 저절로 가지치기 당하게 된다.

이렇게 해서 모든 한 점에서 시작하여 모든 인접한 간선을 조사한 후 가장 최단경로로 갈 수 있는 경우의 수를 조사하는 알고리즘이 다익스트라 알고리즘이다.
백준에 있는 다익스트라 알고리즘을 활용하여 푸는 문제 중 1753번 최단경로 라는 문제의 정답을 약간 변형해서 가져왔다.
대표적인 다익스트라 문제이며 가장 스탠다드한 풀이이다.
#include<bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; // 시작 노드에서 해당 노드까지의 경로가 없는 경우의 비용 #define MAX_VERTEX 1001 // 최대 vertex 개수 #define MAX_EDGE 1001 // 최대 edge 개수 int v, e, start_node; //최소 비용 배열 int d[MAX_VERTEX]; //간선 정보를 담은 vector //index : 시작노드 //value : pair<비용, 도착 노드> 목록 vector<pair<int, int>> edge[MAX_EDGE]; void dijkstra(int start_node) { //시작 노드에서 시작 노드로 가는 비용은 0 d[start_node] = 0; //시작 노드부터 어떤 도착 노드까지의 최소 비용을 제시하는 간선 목록 //pair<비용, 도착 노드> 형식의 우선순위 큐이다. priority_queue<pair<int, int>> pq; //시작 노드에서 시작 노드로 가는 경로와 비용을 pq에 삽입; pq.push({0, start_node}); //pq의 모든 경로를 확인할 때 까지 반복 while(!pq.empty()) { int cur = pq.top().second; int cost = -pq.top().first; //오름차순 정렬을 위해 -를 붙혀서 넣어줬기 때문에 다시 원래값으로 돌림 pq.pop(); if(d[cur] < cost) { continue; } for(int i = 0; i < edge[cur].size(); ++i) { int next = edge[cur][i].second; int nextCost = cost + edge[cur][i].first; if(d[next] > nextCost) { d[next] = nextCost; pq.push({-nextCost, next}); //오름차순 정렬을 위해 -를 붙혀서 넣어줌 } } } } int main() { cin >> v >> e; cin >> start_node; for(int i = 1; i <= v; i++) { d[i] = INF; } while(e--) { int start, end, cost; cin >> start >> end >> cost; edge[start].push_back({cost, end}); } dijkstra(start_node); for(int i = 1; i < v + 1; ++i) { if(d[i] == INF) { cout << "INF" << "\n"; } else { cout << d[i] << "\n"; } } }
3. 시간복잡도
간선의 수를 E(Edge), 노드의 수를 V(Vertex)라고 했을 때 O(E logV)가 된다.
우선순위 큐에서 꺼낸 노드는 서로 인접한 노드만 탐색하므로 최악의 경우라도 총 간선 수인 E만큼만 반복한다. 즉 하나의 간선에 대해서는 O(logE)이고, E는 V2보다 항상 작기 때문에 E개의 간선을 우선순위 큐에 넣었다 빼는 최악의 경우에 대해서는 O(E logV)가 된다.
4. 추천 문제
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 유니온 파인드 / Union-Find (0) | 2023.10.01 |
|---|---|
| [Algorithm] 이분탐색 / Binary Search (0) | 2023.09.25 |
| [Algorithm] 위상정렬 / Topological Sort (0) | 2023.09.22 |
| [Algorithm] 투포인터 / Two Pointers (0) | 2023.08.21 |
| [Algorithm] 동적 계획법 / Dynamic Programming (0) | 2023.06.19 |
