1. 이분탐색이란?
- 이분 탐색 알고리즘은 정렬되어 있는 배열에서 탐색 범위를 절반씩 줄여가며 데이터를 탐색하는 알고리즘이다.
- 이분탐색은 결정 문제의 답이 이분적일 때 사용할 수 있는데 대표적인 예시로 카드 뽑기 문제가 있다. 결정 문제란 답이 Yes or No인 문제를 의미한다.
- 시간 복잡도 : O(logN)
카드 뽑기 문제는 1 ~ 50까지 오름차순으로 정렬된 카드묶음에서 28번 카드를 찾는 문제를 예시로 들어보겠다.
첫번째 카드부터 n번째 카드는 card[i], 우리가 찾고자 하는 카드인 28은 val로 가정한다.
이때 문제를 푸는 방법에 v[i] >= val 인가를 잡으면 답은 1~27까지는 False, 28이후로는 True가 나오게된다. 이때 우리가 찾고자 하는 값은 처음으로 card[i] >= val인 지점 즉 처음 결정 문제의 답이 True로 나오게 되는 위치이다. 이부분이 C++의 STL에 있는 lower_bound값이다.
이렇게 결정문제의 파라미터(이 경우 i, 쉽게 인덱스)에 대해 결정 문제의 답이 두 구간으로 나뉘는 것을 '이분적이다' 라고 하며 이런 경우 이분탐색을 통해 결정 문제의 답이 달라지는 경계를 찾을 수 있다.
2. Default Logic
1. 사용하는 변수
이분탐색을 구현하기위해 필요한 변수에 대해 짧게 설명하고 변수명으로 설명을 진행할 것이다.
low : 탐색하는 구간의 최좌측값
high : 탐색하는 구간의 최우측값
mid : low와 high의 중간 값
2. 구현 방법
이전에 이분탐색은 결정문제의 답이 두 구간으로 나뉘는 부분을 찾는 것이라고 했다. 우선 초기상태의 low, high가 low != high기 때문에 우리가 탐색하는 구간인 [low, high]사이에 결정문제의 답이 바뀌는 구간이 무조건 있음이 보장된다. 결정 문제의 답이 바뀌는 부분은 low + 1 >= high이기 때문에 low + 1 < high인 구간 동안 [low, mid], [mid, high]로 탐색 부분을 줄여나간다. 이때 low + 1 < high를 항상 만족하기 때문에 low와 high 사이에는 항상 한개 이상의 칸이 있음이 보장된다.
(반복문을 탈출했다면 low + 1 >= high인데 low < mid < high인 mid를 대입하기 때문에 low < high이고, 두 조건을 만족하는 low, high는 low + 1 == high인 경우 밖에 없다.)
이후 이분 탐색이 끝나면 low, high는 결정 문제의 답이 바뀌는 경계에 위치하게 되며, 만약 결정 문제 답의 분포가 F~ T인데 정답이 가장 큰 F라면 low를 가장 작은 T라면 high를 출력해주면 된다.
그림으로 알아보자
- 경계를 포함하도록, 즉 Check(low) != Check(high)가 되도록 [low, high]를 잡는다
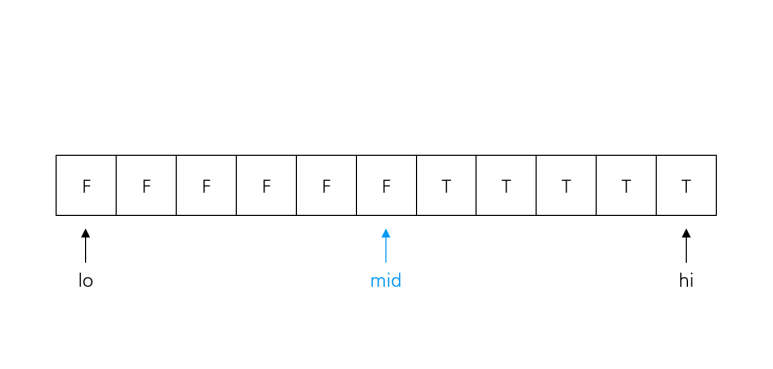
2. Check(low) == mid라면 low = mid, 아니라면 hi = mid를 반복한다.
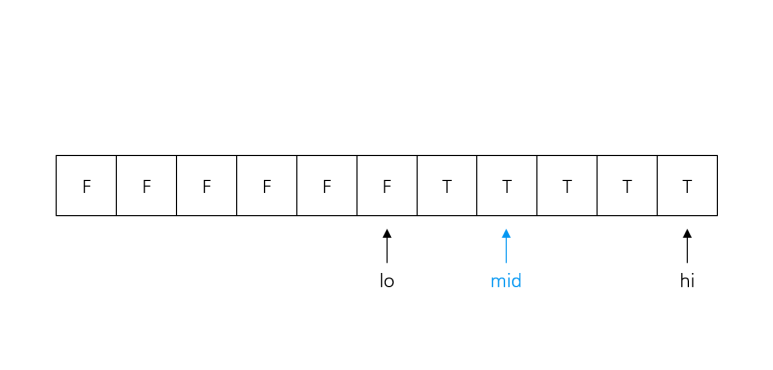
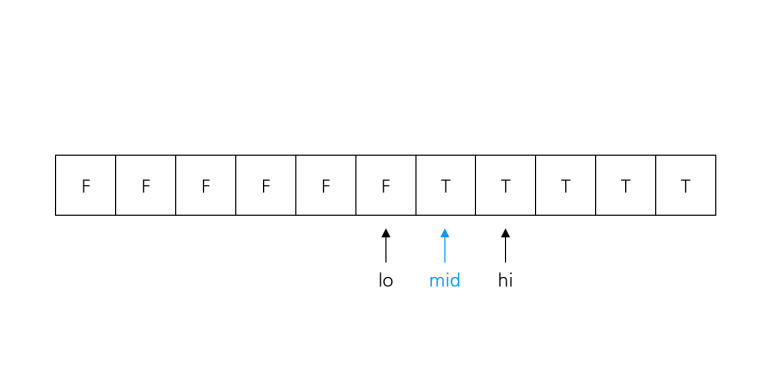
3. low + 1 == hi가 되면 탈출, low, high는 경계에 위치한다.
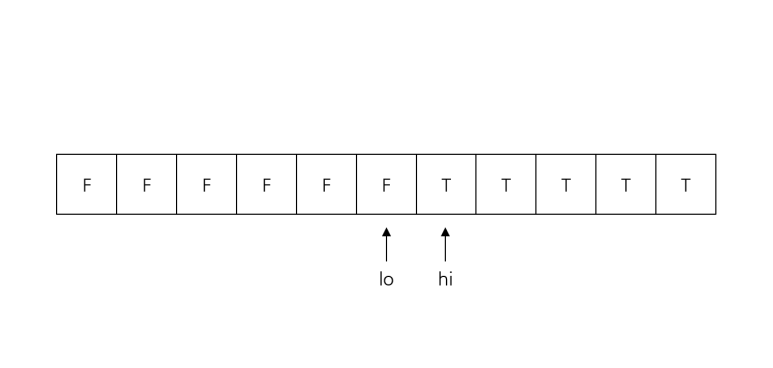
binarySearch() {
int low = 0;
int high = 987654321;
int mid;
while(low + 1 < high) {
mid = (low + high) / 2;
if(target > arr[mid])
low = mid;
else
high = mid;
}
return high;
}
참고 : https://www.acmicpc.net/blog/view/109#comment-718
이분 탐색(Binary Search) 헷갈리지 않게 구현하기
개요 이분 탐색은 off-by-one error가 발생하기 쉬워서 늘 헷갈립니다. 이분 탐색 문제를 풀다보면 탈출 조건으로 lo <= hi, lo < hi, lo + 1 < hi 중 어느 걸 선택해야 할 지, 정답이 lo인지 hi인지 (lo + hi) / 2
www.acmicpc.net
설명을 엄청 잘해주셔서 이분 블로그를 참고해서 작성했다.
3. 추천 문제
https://www.acmicpc.net/problem/2805
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
https://www.acmicpc.net/problem/1654
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Sort() & compare 함수 :: C++ (1) | 2023.12.24 |
|---|---|
| [Algorithm] 유니온 파인드 / Union-Find (0) | 2023.10.01 |
| [Algorithm] 위상정렬 / Topological Sort (0) | 2023.09.22 |
| [Algorithm] 다익스트라 알고리즘 / Dijkstra (0) | 2023.08.30 |
| [Algorithm] 투포인터 / Two Pointers (0) | 2023.08.21 |
1. 이분탐색이란?
- 이분 탐색 알고리즘은 정렬되어 있는 배열에서 탐색 범위를 절반씩 줄여가며 데이터를 탐색하는 알고리즘이다.
- 이분탐색은 결정 문제의 답이 이분적일 때 사용할 수 있는데 대표적인 예시로 카드 뽑기 문제가 있다. 결정 문제란 답이 Yes or No인 문제를 의미한다.
- 시간 복잡도 : O(logN)
카드 뽑기 문제는 1 ~ 50까지 오름차순으로 정렬된 카드묶음에서 28번 카드를 찾는 문제를 예시로 들어보겠다.
첫번째 카드부터 n번째 카드는 card[i], 우리가 찾고자 하는 카드인 28은 val로 가정한다.
이때 문제를 푸는 방법에 v[i] >= val 인가를 잡으면 답은 1~27까지는 False, 28이후로는 True가 나오게된다. 이때 우리가 찾고자 하는 값은 처음으로 card[i] >= val인 지점 즉 처음 결정 문제의 답이 True로 나오게 되는 위치이다. 이부분이 C++의 STL에 있는 lower_bound값이다.
이렇게 결정문제의 파라미터(이 경우 i, 쉽게 인덱스)에 대해 결정 문제의 답이 두 구간으로 나뉘는 것을 '이분적이다' 라고 하며 이런 경우 이분탐색을 통해 결정 문제의 답이 달라지는 경계를 찾을 수 있다.
2. Default Logic
1. 사용하는 변수
이분탐색을 구현하기위해 필요한 변수에 대해 짧게 설명하고 변수명으로 설명을 진행할 것이다.
low : 탐색하는 구간의 최좌측값
high : 탐색하는 구간의 최우측값
mid : low와 high의 중간 값
2. 구현 방법
이전에 이분탐색은 결정문제의 답이 두 구간으로 나뉘는 부분을 찾는 것이라고 했다. 우선 초기상태의 low, high가 low != high기 때문에 우리가 탐색하는 구간인 [low, high]사이에 결정문제의 답이 바뀌는 구간이 무조건 있음이 보장된다. 결정 문제의 답이 바뀌는 부분은 low + 1 >= high이기 때문에 low + 1 < high인 구간 동안 [low, mid], [mid, high]로 탐색 부분을 줄여나간다. 이때 low + 1 < high를 항상 만족하기 때문에 low와 high 사이에는 항상 한개 이상의 칸이 있음이 보장된다.
(반복문을 탈출했다면 low + 1 >= high인데 low < mid < high인 mid를 대입하기 때문에 low < high이고, 두 조건을 만족하는 low, high는 low + 1 == high인 경우 밖에 없다.)
이후 이분 탐색이 끝나면 low, high는 결정 문제의 답이 바뀌는 경계에 위치하게 되며, 만약 결정 문제 답의 분포가 F~ T인데 정답이 가장 큰 F라면 low를 가장 작은 T라면 high를 출력해주면 된다.
그림으로 알아보자
- 경계를 포함하도록, 즉 Check(low) != Check(high)가 되도록 [low, high]를 잡는다

2. Check(low) == mid라면 low = mid, 아니라면 hi = mid를 반복한다.


3. low + 1 == hi가 되면 탈출, low, high는 경계에 위치한다.

binarySearch() { int low = 0; int high = 987654321; int mid; while(low + 1 < high) { mid = (low + high) / 2; if(target > arr[mid]) low = mid; else high = mid; } return high; }
참고 : https://www.acmicpc.net/blog/view/109#comment-718
이분 탐색(Binary Search) 헷갈리지 않게 구현하기
개요 이분 탐색은 off-by-one error가 발생하기 쉬워서 늘 헷갈립니다. 이분 탐색 문제를 풀다보면 탈출 조건으로 lo <= hi, lo < hi, lo + 1 < hi 중 어느 걸 선택해야 할 지, 정답이 lo인지 hi인지 (lo + hi) / 2
www.acmicpc.net
설명을 엄청 잘해주셔서 이분 블로그를 참고해서 작성했다.
3. 추천 문제
https://www.acmicpc.net/problem/2805
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
https://www.acmicpc.net/problem/1654
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Sort() & compare 함수 :: C++ (1) | 2023.12.24 |
|---|---|
| [Algorithm] 유니온 파인드 / Union-Find (0) | 2023.10.01 |
| [Algorithm] 위상정렬 / Topological Sort (0) | 2023.09.22 |
| [Algorithm] 다익스트라 알고리즘 / Dijkstra (0) | 2023.08.30 |
| [Algorithm] 투포인터 / Two Pointers (0) | 2023.08.21 |
