1. Dynamic Programming 이란?
- Dynamic Programming 즉 동적 계획법은 하나의 큰 문제를 여러개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것.
- 내가 이해한 DP란 재귀를 활용하게 되면 알고리즘 문제를 풀 때 이미 계산한 값도 중복해서 계산을 해야 하지만 DP는 내가 생성한 DP테이블에 계산한 값을 저장해 놓기 때문에 동일한 연산을 마주치면 값을 계산하지 않고 dp테이블에서 가져와서 하위 연산을 하지 않기 때문에 시간복잡도를 줄일 수 있음.
- 동적계획법이라고 하기보단 "memoization / 값 저장해서 필요할 때 가져오는 방법" 이라고 이해하면 편할 것 같다
2. DP와 재귀 연산횟수 비교 (백준 2576 계단 오르기)
해당 문제 또한 DP로 풀이해야 하는 대표 문제이다.
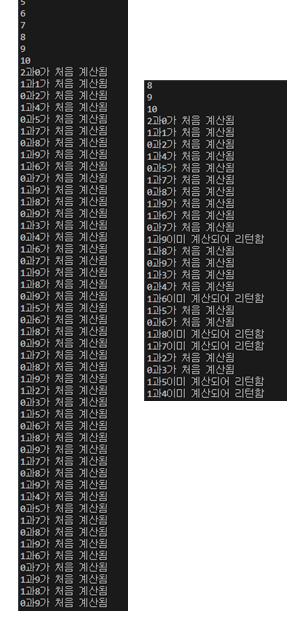
DP를 처음 공부하는 과정에서 연산속도의 차이를 체감하지 못했고 실제로 찍어보며 눈으로 확인했다.
//DP 사용
#include<bits/stdc++.h>
using namespace std;
vector<int> stairs;
int dp[3][301];
int N;
int sum = 0;
int solve(const int n, const int cnt) {
if(cnt == N) return stairs[cnt];
if(cnt > N) return -987654321;
int &ret = dp[n][cnt];
if(ret != -1) {
cout << n << "과" << cnt << "이미 계산되어 리턴함\n";
return ret;
}
ret = 0;
cout << n << "과" << cnt << "가 처음 계산됨\n";
// 앞으로 밟을 계단의 수가 0일때
// 무조건 두 칸 올라가야 됨
if(n == 0) {
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
// 두칸을 올라가고 n을 초기화하거나
// 한칸을 올라가고 다음에 두칸을 뛰어넘던가
else if(n == 1) {
ret = max(ret, solve(0, cnt + 1) + stairs[cnt]);
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
// 시작게단은 계단으로 치지 않기 때문에 n = 2로 설정
else if(n == 2) {
ret = max(ret, solve(1, cnt + 1) + stairs[cnt]);
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
return ret;
}
int main() {
memset(dp, -1, sizeof(dp));
cin >> N;
stairs.push_back(0);
for(int i = 0; i < N; i++) {
int j;
cin >> j;
stairs.push_back(j);
}
cout << solve(2, 0);
}// DP 미사용
#include<bits/stdc++.h>
using namespace std;
vector<int> stairs;
int dp[3][301];
int N;
int sum = 0;
int solve(const int n, const int cnt) {
if(cnt == N) return stairs[cnt];
if(cnt > N) return -987654321;
/*int &ret = dp[n][cnt];
if(ret != -1) {
//cout << n << "과" << cnt << "이미 계산되어 리턴함\n";
return ret;
} */
int ret = 0;
cout << n << "과" << cnt << "가 처음 계산됨\n";
// 앞으로 밟을 계단의 수가 0일때
// 무조건 두 칸 올라가야 됨
if(n == 0) {
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
// 두칸을 올라가고 n을 초기화하거나
// 한칸을 올라가고 다음에 두칸을 뛰어넘던가
else if(n == 1) {
ret = max(ret, solve(0, cnt + 1) + stairs[cnt]);
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
// 시작게단은 계단으로 치지 않기 때문에 n = 2로 설정
else if(n == 2) {
ret = max(ret, solve(1, cnt + 1) + stairs[cnt]);
ret = max(ret, solve(1, cnt + 2) + stairs[cnt]);
}
return ret;
}
int main() {
memset(dp, -1, sizeof(dp));
cin >> N;
stairs.push_back(0);
for(int i = 0; i < N; i++) {
int j;
cin >> j;
stairs.push_back(j);
}
cout << solve(2, 0);
}
3. 추천 문제
https://www.acmicpc.net/problem/1463
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
https://www.acmicpc.net/problem/9095
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
https://www.acmicpc.net/problem/1149
1149번: RGB거리
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
https://www.acmicpc.net/problem/11726
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
코드에서 잘 이해가 안가는 부분은 댓글로 남겨주시면 최대한 찾아서 알려드리겠습니다!
조금이라도 최적화를 할 수 있거나 다른 의견도 댓글에 남겨주세요!
지적과 비판 새로운 의견은 항상 환영합니다👍
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 유니온 파인드 / Union-Find (0) | 2023.10.01 |
|---|---|
| [Algorithm] 이분탐색 / Binary Search (0) | 2023.09.25 |
| [Algorithm] 위상정렬 / Topological Sort (0) | 2023.09.22 |
| [Algorithm] 다익스트라 알고리즘 / Dijkstra (0) | 2023.08.30 |
| [Algorithm] 투포인터 / Two Pointers (0) | 2023.08.21 |
