728x90
반응형
1. Tree / 트리
- 한개 이상의 노드로 이루어진 유한 집합이며, 비선형 자료구조이다.
- 하나의 루트 노드 아래에 0개 이상의 자식 노드로 구성된다. 그리고 그 자식 또한 0개 이상의 자식 노드를 가지고있고 무한히 반복가능하다.
- 컴퓨터의 디렉터리 구조가 대표적인 트리 구조로 이루어져 있다!
1-2. Tree 용어
- 루트 노드(root node) : 부모가 없는 노드. 트리에는 오직 하나의 루트 노드만이 존재한다.
- 리프 노드, 단말 노드(leaf node, terminal node) : 자식이 없는 최말단 노드
- 내부 노드, 비단말 노드(internal node, nonterminal node) : 단말 노드를 제외한 나머지 노드
- 가지, 링크(branch, link, edge) : 노드와 노드를 연결하는 선. 노드가 N개인 트리는 항상 N-1개의 링크를 가진다.
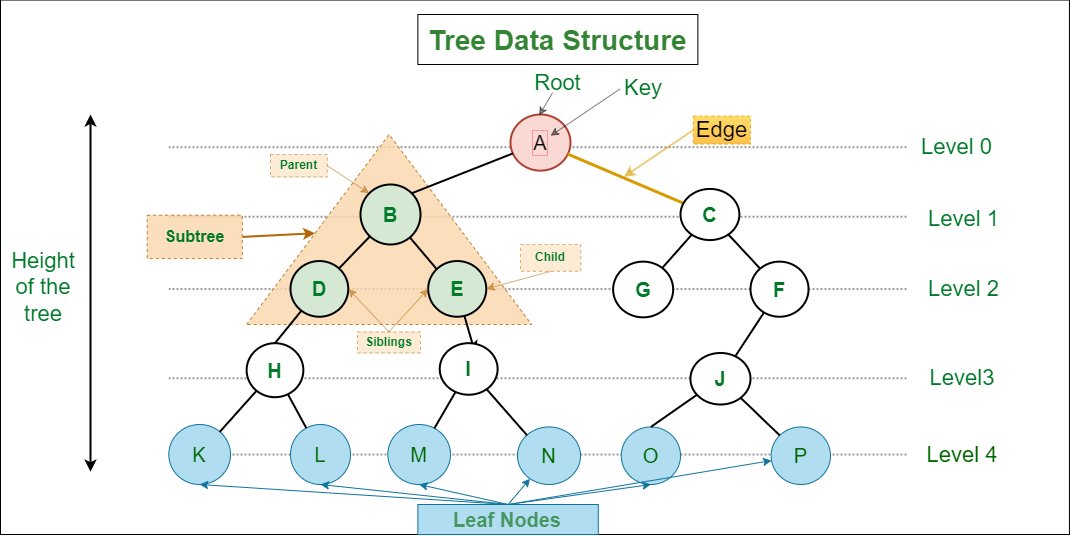
- 형제(sibling) : 같은 부모를 가지는 노드
- D와 E는 B를 부모로 가지는 형제노드이다.
- 노드의 크기(size) : 자신을 포함한 모든 자식 노드의 갯수
- B의 크기 : 9
- J의 크기 : 3
- 노드의 깊이(depth) : 루트노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- B의 깊이 : 1
- H의 깊이 : 3
- 노드의 레벨(Level) : 트리의 특정 깊이를 가지는 노드의 집단
- F의 레벨 : 2
- 노드의 차수(degree) : 노드가 가진 간선의 갯수
- E의 차수 : 1
- C의 차수 : 2
- 트리의 차수 : 트리의 최대 차수
- 트리의 높이 : 루트 노드로부터 가장 깊숙히 있는 노드의 깊이
- A트리의 높이 : 4
2. Binary Tree / 이진 트리
- 각 노드는 최대 2개의 자식을 가진다.
- 2개의 자식은 각각 왼쪽 자식, 오른쪽 자식으로 나뉜다.
2-2. 트리의 종류
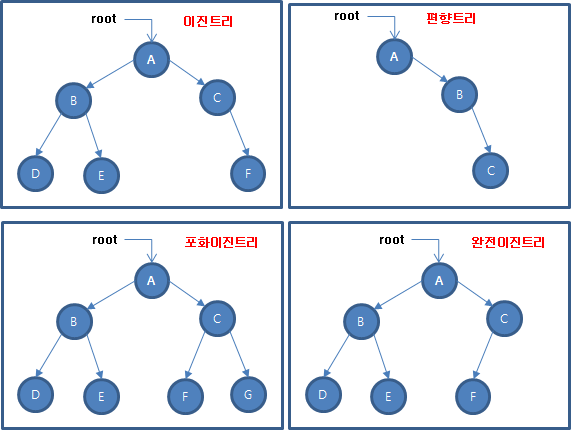
- 편향 트리
- 같은 높이의 이진 트리 중에서 최소 갯수의 노드를 가지면서 왼쪽 혹은 오른쪽 서브 트리만을 가지는 이진 트리
- 편향 트리에서 값 검색 시 시간 복잡도 : O(N)
- 노드의 갯수만큼 재귀를 호출해야 하기 때문에 검색에 불리함.
- 포화 이진트리
- 모든 레벨의 노드가 꽉 차있는 이진트리
- 트리의 노드 갯수 : $2^h-1$ (h = 트리의 높이, h>= 1)
- 완전 이진 트리
- 마지막 레벨을 제외하고 나머지 레벨의 노드가 모두 채워져있는 트리
- 높이가 h일 때 1~h-1까지는 포화 이진트리, h는 왼쪽 먼저 채워져 있어야 함.
- 왼쪽 노드 없이 오른쪽 노드만 있으면 완전 이진 트리의 조건 불만족
CS 지식을 공부하고 기록하는 개인 공부 블로그입니다.
내용 중 틀린 부분 피드백 혹은 궁금한 점이 있으면 댓글로 남겨주시면 참고 및 답변 달아드리겠습니다🧐
728x90
반응형
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 트리의 순회 방법 - 전위, 중위, 후위, 레벨 (0) | 2024.01.11 |
|---|---|
| [자료구조] Linked list를 활용한 이진 트리 구현 :: C++ (1) | 2024.01.11 |
| [자료구조] Doubly Linked List / 이중 연결 리스트 구현 :: C++ (0) | 2023.12.15 |
| [자료구조] Singly Linked List/단일 연결 리스트 & 단일 연결 리스트 구현 :: C++ (0) | 2023.12.12 |
| [자료구조] Queue/큐 & 배열을 통한 큐 구현 :: C++ (0) | 2023.12.10 |
728x90
반응형
1. Tree / 트리
- 한개 이상의 노드로 이루어진 유한 집합이며, 비선형 자료구조이다.
- 하나의 루트 노드 아래에 0개 이상의 자식 노드로 구성된다. 그리고 그 자식 또한 0개 이상의 자식 노드를 가지고있고 무한히 반복가능하다.
- 컴퓨터의 디렉터리 구조가 대표적인 트리 구조로 이루어져 있다!

1-2. Tree 용어
- 루트 노드(root node) : 부모가 없는 노드. 트리에는 오직 하나의 루트 노드만이 존재한다.
- 리프 노드, 단말 노드(leaf node, terminal node) : 자식이 없는 최말단 노드
- 내부 노드, 비단말 노드(internal node, nonterminal node) : 단말 노드를 제외한 나머지 노드
- 가지, 링크(branch, link, edge) : 노드와 노드를 연결하는 선. 노드가 N개인 트리는 항상 N-1개의 링크를 가진다.

- 형제(sibling) : 같은 부모를 가지는 노드
- D와 E는 B를 부모로 가지는 형제노드이다.
- 노드의 크기(size) : 자신을 포함한 모든 자식 노드의 갯수
- B의 크기 : 9
- J의 크기 : 3
- 노드의 깊이(depth) : 루트노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- B의 깊이 : 1
- H의 깊이 : 3
- 노드의 레벨(Level) : 트리의 특정 깊이를 가지는 노드의 집단
- F의 레벨 : 2
- 노드의 차수(degree) : 노드가 가진 간선의 갯수
- E의 차수 : 1
- C의 차수 : 2
- 트리의 차수 : 트리의 최대 차수
- 트리의 높이 : 루트 노드로부터 가장 깊숙히 있는 노드의 깊이
- A트리의 높이 : 4
2. Binary Tree / 이진 트리
- 각 노드는 최대 2개의 자식을 가진다.
- 2개의 자식은 각각 왼쪽 자식, 오른쪽 자식으로 나뉜다.
2-2. 트리의 종류

- 편향 트리
- 같은 높이의 이진 트리 중에서 최소 갯수의 노드를 가지면서 왼쪽 혹은 오른쪽 서브 트리만을 가지는 이진 트리
- 편향 트리에서 값 검색 시 시간 복잡도 : O(N)
- 노드의 갯수만큼 재귀를 호출해야 하기 때문에 검색에 불리함.
- 포화 이진트리
- 모든 레벨의 노드가 꽉 차있는 이진트리
- 트리의 노드 갯수 : $2^h-1$ (h = 트리의 높이, h>= 1)
- 완전 이진 트리
- 마지막 레벨을 제외하고 나머지 레벨의 노드가 모두 채워져있는 트리
- 높이가 h일 때 1~h-1까지는 포화 이진트리, h는 왼쪽 먼저 채워져 있어야 함.
- 왼쪽 노드 없이 오른쪽 노드만 있으면 완전 이진 트리의 조건 불만족
CS 지식을 공부하고 기록하는 개인 공부 블로그입니다.
내용 중 틀린 부분 피드백 혹은 궁금한 점이 있으면 댓글로 남겨주시면 참고 및 답변 달아드리겠습니다🧐
728x90
반응형
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 트리의 순회 방법 - 전위, 중위, 후위, 레벨 (0) | 2024.01.11 |
|---|---|
| [자료구조] Linked list를 활용한 이진 트리 구현 :: C++ (1) | 2024.01.11 |
| [자료구조] Doubly Linked List / 이중 연결 리스트 구현 :: C++ (0) | 2023.12.15 |
| [자료구조] Singly Linked List/단일 연결 리스트 & 단일 연결 리스트 구현 :: C++ (0) | 2023.12.12 |
| [자료구조] Queue/큐 & 배열을 통한 큐 구현 :: C++ (0) | 2023.12.10 |
